2 minute read

I’ve been dealing with proofs by induction in my coursework. I know how it works. But I never really understood why it worked. I searched a bit online and I think I understand why it works. So here goes -

What it means to prove a logical implication:

Logical implication looks like $P \implies Q$. Here, the antecedent is P and consequent is Q.

The following truth table for implication might seem familiar -

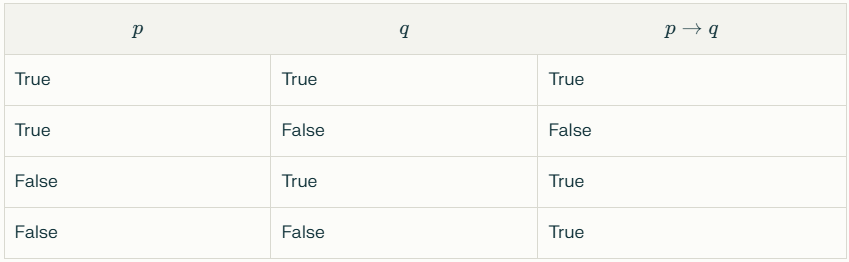
Truth table of logical implication

As can be seen from the table, an implication only makes claims for the case when the antecedent P is true.

  • When P is true, Q has to be true for the implication $P \implies Q$ to be true.

  • When P is true and Q is false, the implication is false.

When P is false however, the implication becomes true vacuously but makes no claims whatsoever about the truth value of Q. Hence, an implication becomes “active” only when the antecedent is true.

If P is true and the implication $P \implies Q$ is true we can conclude that Q has to be true.

Using implication to understand why Induction proofs work:

In induction proofs we usually wish to prove a certain property say (X) for an infinite number of values. Consider an induction proof where we use induction to prove that X is satisfied by all natural numbers 0, 1, 2…

  • Base case: The base case would involve proving that X(0) is true. This is usually trivial.

  • Inductive step: This is where implication plays a crucial role. The versions of induction proofs I have seen state that we need to assume X(k) is true for some k and using this we need to prove that X(k+1) is also true.

    This in fact is simply asking us to provide the direct proof for the implication $X(k) \implies X(k+1)$ where we need to assume X(k) is true and prove X(k+1) is true.

    This however, doesn’t change the fact that the inductive step simply needs us to prove the implication $X(k) \implies X(k+1)$. We can choose to prove this implication in whichever way we may want (Proof by contradiction, Direct proof, proof by contraposition and so on.)

Now, assume that we manage to prove the implication. This has the following consequences -

  • X(0) is true (base case) and $X(0) \implies X(1)$ is true. Thus, X(1) has to be true.

  • X(1) is true and $X(1) \implies X(2)$ is true. Thus, X(2) has to be true.

  • And so on…

We can thus see how logical implication plays a crucial role in establishing the correctness of a proof by induction.

You May Also Enjoy